My Ortvay Problems and Solutions
The International Ortvay Competition in Physics is one of the most popular university level theoretical physics competitions in Hungary. For a brief discription see my page on the Ortvay Seminar. The selected problems are either ones which I had proposed for the competition, or those which I solved as a contestant.
The problems are sorted by topic:
2004. Problem 13.
Water is rotated at a constant angular velocity omega in a cylindrical tank. A uniform wooden ball of radius R, stationary in the reference frame co-rotating with the water is placed into the water. Where will the ball be after a long period of time? Study the case of small balls, as well as bigger ones, for which R >~ g / omega.
2001. Problem 9.
A long iron rod is stretched longitudinally, fixed, and then encapsulated in a hot cylindrical concrete, which is coaxial with the rod and has length L. After the concrete has hardened, the rod is stopped to be pulled at its ends. Determine the strain and the stress in the assembly. Assume that the concrete and the iron stick to each other perfectly.
Download my solution (in Hungarian)
2001. Problem 8.
Two identical electric line posts are separated by 50 meters. A steel cable is spanned between the top of the posts. The maximum slack of the cable (i.e. the vertical distance between the ends and the middle of the cable) is 1 meter. How large will the maximum slack of the cable be when a pigeon weighing the amount of 2 meters of cable settles down at halfway between the posts?
Download my solution (in Hungarian)
2001. Problem 6.
A point-like particle is moving in a central force field V(r). Following its motion for a while it is surprising to see that it moves along a circular arc of radius rho that is not concentric, i.e. its center is at a distance R > rho from the center of the force field. Determine the potential function V(r). What is the complete trajectory of the particle?
Download my solution (in Hungarian)
2001. Problem 4.
An aircraft is gliding calmly in the night sky, when suddenly all electronics pack up (Y2K bug?), except for the steering equipment and the driving gear. The pilot cannot see or hear a thing. She can rely solely on her senses, her middle ear (which is sensitive for accelerations). She tries to maneuver in such a manner that she should always feel a "vertical" acceleration of 1g.
a) At what speed will the plane hit the ground if initially it was traveling horizontally at 800 km/h, at an altitude of 4000 m, but was deflected due to some slight perturbation?
b) Provided the above conditions, what trajectories can the plane follow? (Focus on planar motions and motions along the lateral surface of a circular cylinder.)
Download my solution (in Hungarian)
2001. Problem 3.
When a forest is lumbered, high and long stacks are built from the timbers that are previously chopped into 1-meter-long saw-logs. At the two ends of the stack large and strong trees are used to support the logs. When there are no trees around, a simple and clever solution is used for preventing the logs from rolling in all directions. A thick (as an arm) Y-shaped bough is placed horizontally among the logs in such a way that its two branches are inside of the stack, and in a horizontal plane, while the branching point is just outside.
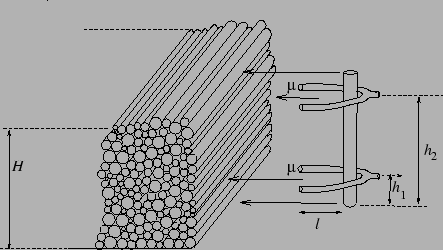Another strong bough is put through the branching vertically (see Fig.) and fixed temporarily; then the two branches of the Y are loaded in several layers with further logs. The vertical bough passes through two Ys, which, due to weight and friction, get stuck in the stack. At what height should the two Y-shaped supports be placed? How high can a stack be built, if the branches of the Ys reach a depth L parallel into the stack? Friction among the logs can be neglected, while the coefficient of friction between the Ys and the logs is mu.
Download my solution (in Hungarian)
2001. Problem 2.
A homogeneous circular disk is lying on a horizontal carpet, exerting a uniform pressure on the carpet. An F_0 force is needed to move the disk in a radial direction with pulling a string (the string is attached to the edge of the carpet). What force is needed to move the disk, if the string is pulled in the tangential direction? (The string is horizontal in both cases.)
Download my solution (in Hungarian)
2000. Problem 9.
An hour-glass is fixed to the end of a weightless rod, and the assembly is swung. The sand keeps pouring continuously down. Determine the motion of the system.
Download my solution (in Hungarian)
2000. Problem 8.
One end of a massive rope of length L is attached to the vertical axis of a motor rotating at an angular velocity w, the other end hangs freely. The motor is turned on. After a long period of time, the rope rotates as a rigid body with angular velocity w. Determine (and plot) the shape of the rope for different angular velocities. Discuss the cases w^2 << g / L, w^2 ~ g / L, and w^2 >> g / L.
Download my solution (in Hungarian)
2000. Problem 6.
One end of a thin, flexible, unstretchable, massless string is clamped, the other is led over a pulley and attached to a massive object (which is hanging on it). A bead, which can slide without friction, is thread onto the originally horizontal piece of string.
a) Determine the potential felt by the bead.
b) Another bead is thread onto the string. What potential is felt by the two beads? How do they interact?
Download my solution (in Hungarian)
2000. Problem 5.
A moving walkway of width d moves at a speed c, while one can walk at a speed v relative to the walkway (which is the same as one's walking speed on the ground.) What trajectory should one follow if one wishes to cross the moving walkway and reach the point across the walkway exactly opposite the starting point? What is the minimum time for the crossing if the speed ratio v / c is a) greater b) less than the golden ratio?
Download my solution (in Hungarian)
2001. Problem 20.
Billy Beery wants to keep the liquid nitrogen cool, which is needed for his experiments, as well as his beer, in the most economical way. He is trying to devise a device that renders non-isothermal processes unfeasible.
"I'll take a tricky shaped funnel closed at its bottom," he thinks aloud. "Then, with a blob of mercury, I trap some gas in the funnel - thus I separate it from the outside. The position of the mercury in the funnel determines not only the volume of the gas inside, but also the thickness of the mercury blob, which in turn determines the gas pressure. All that is left is to find a suitably shaped funnel in which the product is kept constant. And then, come hell or high water, the gas temperature simply cannot change."
Help Billy to find the suitable shape of the funnel.
Download my solution (in Hungarian)
2000. Problem 15.
Determine the efficiency of a heat engine with two heat reservoirs (of temperature T_0 and T_1), if heat transfer between the engine and the reservoirs is due to heat conduction, and maximum performance is assumed. The law for heat conduction is linear: dQ/dt = (T_1-T_0) R.
Download my solution (in Hungarian)
2004. Problem 15.
Once upon a time, when the weather was particularly windy, Huygens, Fresnel, and Bernoulli went to the prairie to play the drum. The instrument was with Huygens, and from time to time he hit it. Fresnel and Bernoulli were listening to Huygens's play from the same distance; Bernoulli against the wind, and Fresnel in the direction of the wind. The wind was blowing horizontally, and its speed varied with the altitude as v=a*z (being much smaller than the sound speed at all heights relevant to the problem). What did Fresnel and Bernoulli hear? (The sound emitted by the drum can be approximated by a short delta pulse; the viscosity of air can be neglected.)
2001. Problem 17.
A thin conducting ring of radius a and resistance R is dropped from height h onto a small magnet of magnetization m resting on a table. Let the m be perpendicular to the surface of the table, and suppose that the axis of the ring stays vertical and points in the direction of the magnet throughout its motion. Describe the motion of the ring. When does it hit the table?
Download my solution (in Hungarian)
2000. Problem 18.
The edges of a cube are made of thin wires of uniform specific resistance. A current of 1 A flows into one of the vertices, and out at another vertex at the other end of a face diagonal. (The input and output wires connecting the cube to the source current are long straight conductors, the lines of which cross the centre of the cube.) What is the magnetic field strength at the centre of the cube? Generalize the problem for the case of other regular polyhedra, e.g. determine the magnetic field strength at the centre of a regular dodecahedron for different relative positions of the entering and exiting currents.
Download my solution (in Hungarian)
2000. Problem 17.
A square lattice of identical resistances (1 ohm along each edge) is wrapped around an infinite cylinder in such a way that N resistances are placed along the cross sectional circle of the cylinder. What are the resultant resistances between two adjacent lattice points in the "axial" and in the "circumferential" directions? First consider the cases N = 2, N = 3, and the limit when N approaches infinity.
Download my solution (in Hungarian)
2002. Problem 23.
According to the special theory of relativity, travelling forward in time is possible, if one leaves Earth (considered stationary), accelerates, reaches almost to the speed of light, and then returns.
a) Plan a journey to visit your twelfth-generation descendant, who lives 300 years hence.
b) Give the shape of a closed loop along which one should travel in space if one wishes to grow older as little as possible by the end of the journey to the twelfth-generation descendant.
c) How much proper time is minimally needed if one wishes to see the universe twice as old as now?
In each case one should return to and stop on the Earth. Do not forget about the tolerance limitations of the human body: the experienced acceleration should not ever exceed g, i.e. the usual acceleration of the Earth's gravity.
2004. Problem 22.
Observations establish the fact that the rotational velocity of the stars in circular orbits around the center of a spiral galaxy does not depend on their distance from the galactic center. Interestingly, this relation holds even for large distances, where only an insignificant amount of luminous matter is present. The standard resolution of this contradiction is to assume the presence of a non-luminous (dark) matter in the galaxy, and the gravitational effects of this dark matter take care of the relation at large distances.
In another possible approach the presence of dark matter is not assumed, but rather Newton's law is modified.Suppose that the gravitational force between two point-like particles is of the form
F = G(r)*m_1*m_2 / r^2 where G(r) is the distance-dependent gravitational constant.
The density distribution of a spiral galaxy can be approximated by rho(R,z)=rho_0 exp(-a*R) delta(z) where R is the distance from the center, and 1 / alpha = 4 kpc, and z is the coordinate perpendicular to the plane of the galactic disc. How should G(r) be chosen so that the density distribution alone may account for the observations of circumferential velocities?
Extra question: Can the above form of G(r) be falsified through observations concerning the solar system only?
2004. Problem 20.
The space travel agency Black Hole Travels organizes exotic trips for adventurous billionaires. Travelers can select the black hole they want to visit from a catalog. The participants are then transported into the vicinity of the black hole on a luxurious space ship, which then starts circling the black hole in a circular orbit. Approaching the horizon of the black hole, the travelers may enjoy a fantastic view: the sky closes in, stars turn blue, etc.
a) How close can they approach the horizon of a static black hole of mass M?
b) How deeply can they enter into the ergosphere of a Kerr black hole of mass rotating at maximum angular momentum, if the acceleration due to gravity should not exceed the usual terrestrial value, and the tidal forces should not make the travelers feel too uncomfortable? Examine the cases M=Msun and M=10^6 Msun.
Contestants should clarify the concept of too uneasy in their solution.
2003. Problem 29.
One signal type that present-day gravitational wave detectors might be able to detect is gravitational bremsstrahlung, created when two compact stars on hyperbolic paths pass by each other. The characteristic frequency of the emitted gravitational radiation is f = v / b, where b is the distance of closest approach, and v is the relative speed in that point. Estimate the rate of gravitational bremsstrahlung signals that are produced by a typical globular cluster within the frequency range of the terrestrial gravitational wave detectors (between 100 and 3000Hz). For simplicity, assume that the cluster contains 10^6 stars, distributed uniformly over a sphere 20 ly across. First study the ``perfect gas'' approximation, and then take into account deflections due to gravitation.
2002. Problem 26.
In the recent decades tremendous amounts of money is being spent world-wide on building gravitational wave detectors. The newly built LIGO (Laser Interferometer Gravitational Wave Observatory, USA) finished its first measurement period last month, however, according to the preliminary disclosure of results, no gravitational wave event has been found. Only signals emitted by the most violent astrophysical sources are expected to exceed the noise limit of the detector. Give an upper limit on the maximum energy emitted in the gravitational wave channel during a supernova explosion. How large must a 100% efficiency interferometer be (at least) in order to detect such a signal?
2001. Problem 7.
Most people love to hike - but the pleasure they take in it differs from one person to the other. Suppose a hiker wants to get from a point A to a point B in a certain amount of time. The relief map of the area is at his disposal, i.e. he knows the function h(r) = h(x,y). (The vectorial quantities should be regarded as two-dimensional, i.e. z components are suppressed.) Our hiker would like to suck as little as possible, where the "suck" function is the time integral of the "labor" function: \int_A^B L dt.
Several different labor functions can be defined. Nobody likes to run around quickly, therefore the first term is proportional to the square of the velocity: L_1 = (1/2) a v^2. Going uphill sucks a lot, while going downhill is cool: L_2 = b (v.g), where v is the hiker's velocity vector, and g = grad h is the gradient function of the terrain. When, however, the hillside is very steep, going downhill is just as difficult as going uphill, therefore: L_3 = c/2 (v.g)^2. (In the above expressions a, b and c are positive constants.)
a) Write up and interpret the hiker's Euler-Lagrange equations for each term above. What are the resulting paths and hiking strategies? Is the "energy" a constant of motion? If so, what is the meaning of "energy conservation"?
b) Consider a balanced hiker, whose labor function is the sum of the three above terms, L = L_1 + L_2 + L_3. He has to get to the around a cone-shaped mountain, i.e. let h(x,y) = - G (x^2 + y^2)^(1/2), where G is a positive constant. Suppose that h_A = h_B. What path should he follow? How should he walk along it?
c) Propose a labor function of your own, with at least one essentially new term. Sketch the implied strategies.
Download my solution (in Hungarian)
2001. Problem 1.
You are in the middle of a huge field, and being bored, you decide to play with your watch. Therefore you put your bent arm in front of your nose, and
a) Each second you turn in the direction of the watch's second hand and make a step forward. (Your arm is kept fixed, ie it turns along with you.) Where will you end up in a minute's time? Describe the described trajectory.
b) You decide to make a step (in the direction of the watch's second hand) only every nth tick. You do not necessarily start off at the minute sharp (i.e. in the 12 o'clock direction). How does the trajectory depend on n and the initial moment? Classify the possible trajectories.
c) What if the watch's second hand is accelerated uniformly, i.e. if it makes an angle phi = (2pi / 60)*(a*t^2 + b*t) with the initial direction, where t = 1, 2, ... is time measured in seconds, and a and b are integers. Do periodic orbits exist?
d) The second hand is not accelerated any more, but it moves continuously, making n rounds per minute (n is an integer), and you also move continually (in the direction of the second hand). Describe the resulting motion.
Download my solution (in Hungarian)
2000. Problem 1.
A solid wooden ball of density 500 kg/ is tied to a dog's tail. The tail, whose mass and thickness are negligible, is 80 cm long and starts at a height of 40 cm. The dog starts running at a speed of 1 m/s. When it hears that the ball has bumped against the ground, it doubles its pace. (This Superdog can run as fast as it desires.)
a) What speed will it reach after a long while?
b) If the density of the ball may be increased at will, what is the limiting speed that our Superdog will never exceed?
Download my solution (in Hungarian)
1999. Problem 34.
When people work, they get tired, and this affects their efficiency, too. Let us model this the following way: Q(t) = P(t) eps(t), where P(t) is the instantaneous performance, eps(t) is the instantaneous efficiency, and Q(t) is the instantaneous effective performance. eps(t) = 1 - f(t), where f(t) is the instantaneous tiredness, which makes our efficiency smaller. If someone is very tired, the efficiency might even be negative, since a zombie rather destroys than does useful work. Tiredness is the cumulative function of the previous performance:
where P_0 and tau are human constants characteristic of the person working.
a) Assume one works at a constant performance. How does one's effective performance change with time? What is one's effective performance after a good while? At what performance value can it be maximized? What is the efficiency in this case? How is this affected by being tired/restful initially? What do the human constants mean?
b) Next, assume that our boss expects us to work with a constant effective performance. How should we change our performance to come up to this expectation? For how long can we persist? What are the human constants preferred by the boss? What happens if someone starts working with a hangover?
c) Suppose a certain amount of work has to be completed in a certain amount of time. What is the best working strategy if we want to complete the task with investing the least possible performance?
Download my solution (in Hungarian)
